Singular Value Decomposition (SVD)
#mathematics #lecture
It can be thought of as a ‘data reduction’ method for reducing vectors in high dimension to lower dimensions. It can also be considered as ‘data-driven generalization of Fourier transform’
When do this kind of transformation, we don’t know what coordinate system to use so we have to tailor it.
Let’s say we have a matrix , SVD allows us to decompose into three matrices . has the same height as the columns are eigen vectors that describes the variance in the original matrix in decreasing ability. has same width as the original matrix. has a diagonal line of with decreasing importance.
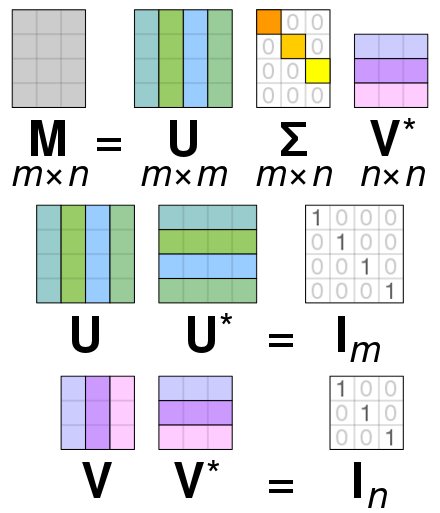 ^[https://en.wikipedia.org/wiki/Singular_value_decomposition]
^[https://en.wikipedia.org/wiki/Singular_value_decomposition]
Since they are ordered by importance, we can chop off some parts of to make things smaller
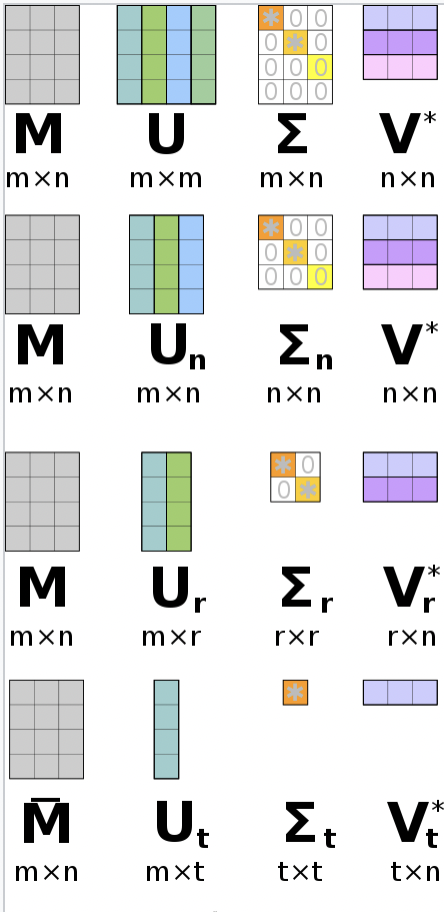 ^[https://en.wikipedia.org/wiki/Singular_value_decomposition]
^[https://en.wikipedia.org/wiki/Singular_value_decomposition]
How to calculate the SVD?
The rigorous way:
#stub
The easy and fast and cheaty way:
in pytorch, run U, S, V = torch.svd(X)
References: